
The Mathematicians or the Young Lady Who Fled: The Dispute Between Doctors Raasbollius and Urinaal, by Cornelis Troost, 1741. Mauritshuis, The Hague.
The four impossible “problems of antiquity”—trisecting an angle, doubling the cube, constructing every regular polygon, and squaring the circle—are catnip for mathematical cranks. Every mathematician who has email has received letters from crackpots claiming to have solved these problems. They are so elementary to state that nonmathematicians are unable to resist. Unfortunately, some think they have succeeded—and refuse to listen to arguments that they are wrong.
Mathematics is not unique in drawing out charlatans and kooks, of course. Physicists have their perpetual-motion inventors, historians their Holocaust deniers, physicians their homeopathic medicine proponents, public health officials their anti-vaccinators, and so on. We have had hundreds of years of alchemists, flat earthers, seekers of the elixir of life, proponents of ESP, and conspiracy theorists who have doubted the moon landing and questioned the assassination of John F. Kennedy.
Circle squarers and angle trisectors have been around for as long as the problems themselves. The ancient Greeks used the word τετραγωνιζειν (tetragonidzein), which translates “to occupy oneself with the quadrature,” to describe those trying to solve the circle-squaring problem.
Augustus De Morgan (1806–1871) wrote numerous columns for the journal Athenæum, which were published posthumously by his wife as Budget of Paradoxes. The subject of these columns? Paradoxers. De Morgan explained, “I use the word [paradox] in the old sense: a paradox was something which was apart from general opinion, either in subject matter, method, or conclusion.” For De Morgan, paradox is not necessarily a pejorative term, and in fact, he labeled Galileo and Copernicus paradoxers. However, he was particularly interested in when the paradoxers were wrong—when they were cranks.
Given his mathematical background, De Morgan wrote extensively about mathematical cranks. He coined a term for this so-called illness that affects these misdirected enthusiasts: “morbus cyclometricus” (“the circle squaring disease”). He wrote,
The feeling which tempts persons to this problem is that which, in romance, made it impossible for a knight to pass a castle which belonged to a giant or an enchanter…When once the virus gets into the brain, the victim goes round the flame like a moth; first one way and then the other, beginning where he ended, and ending where he begun.
The first use of the word crank in the scientific sense may be in a 1906 book review in Nature. The reviewer played off the notion of a crank that you would turn:
A crank is defined as a man who cannot be turned. These men [flat earthers, circle squarers, and trisectors] are all cranks; at all events, we have never succeeded in convincing one of them that he was wrong. The usually accepted axioms, definitions, and technical terms are not for them. Whether they use a term, sometimes evidently in two different senses in the same syllogism, it is impossible to find exactly what they mean by it. (Brackets in original)
The term was well established by the middle of the twentieth century. Nobel Laureate John Nash Jr. (1928–2015), the subject of the popular book and film A Beautiful Mind, used the term in a January 1955 letter to the National Security Agency. Nash was following up on a letter he’d written in which he proposed an encryption–decryption device. The first letter had gone unanswered. His reply assured them, “I hope my handwriting, etc. do not give the impression I am just a crank or circle-squarer.”

In 1931 the Reverend Jeremiah J. Callahan (1878–1969) became the fifth president of Duquesne University in Pennsylvania, and he almost immediately caused a stir by claiming that he could trisect an angle using only a compass and straightedge. (He also published a controversial book called Euclid or Einstein: A Proof of the Parallel Theory and a Critique of Metageometry in which he supposedly proved Euclid’s parallel postulate—another impossible task that is a favorite of mathematical cranks—and attacked Einstein for his theories’ reliance on non-Euclidean geometry.) However, Callahan refused to share his trisection technique, saying that he wanted to wait until he obtained a copyright. Presumably, he thought the proof so valuable that he dared not share it, lest someone else claim credit for it.
News of his trisection was widely reported throughout the country, including an announcement in Time magazine. The Pittsburgh Press cited the mathematician Eric Temple Bell (1883–1960), who pointed out, correctly, that the problem was proved impossible in 1837. In response, Callahan was quoted as saying, “It is his privilege to think what he likes. This problem was just like many others that have been declared impossible of solution. A solution has been found.”
Eventually, Callahan shared his so-called proof. Instead of trisecting an arbitrary angle, he gave a convoluted method of tripling an angle. In other words, he began with an angle ∠BDC and he constructed an angle ∠BDE so that ∠BDC = ⅓∠BDE.
Peruse the writings of mathematical cranks and we find many different, creatively incorrect methods of trisecting angles and squaring circles. The flaws in some proofs are immediately obvious to any mathematically trained reader—like Callahan’s angle tripling. Other proofs are trickier to unravel—often because the writer presents a complicated mess of symbols, diagrams, and terminology. Also, sometimes the incorrect technique produces a good approximation. It is easy to be fooled by a convincing diagram.
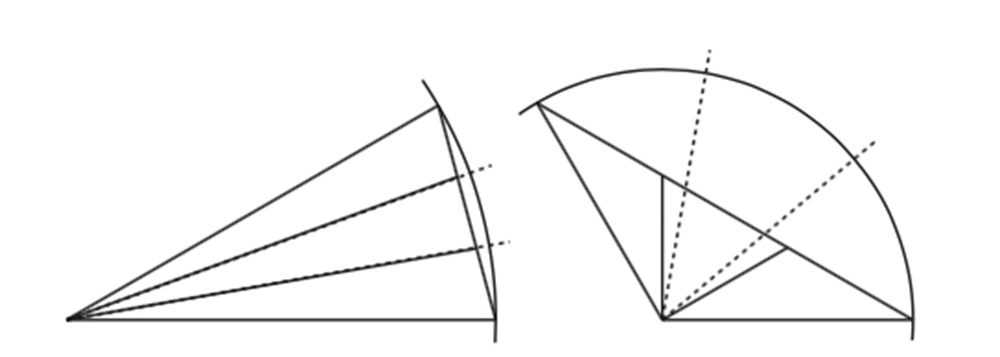
The figure below shows a common angle trisection argument. Draw a circle with its center at the vertex of the angle. Draw the chord determined by the angle. It is possible to trisect a line segment—and hence, this chord—using a compass and straightedge. Then draw the segments from the vertex of the angle to the trisection points. If only angle trisection was that simple! As we see in the figure, if the angle is small—or even not so small—the procedure looks accurate (the dashed lines are the sought-after segments). But as the angle gets larger, it becomes apparent that trisecting the chord does not trisect the angle.
Many circle squarers are fixated on finding the “true” value of π. Among the candidates are 3 or 3.1 or 3.2 or 22/7 or √10 and so on. Through incorrect mathematics, deceptive figures, and approximations, they obtain rational or certain irrational values of π that can be constructed with a compass and straightedge.
Others mistake an example for a proof. It is possible to trisect some angles—45º, 90º, 180º, and so on. Thus, some cranks put forward these constructions as evidence that they can solve the general problem.
Unfortunately, many of these cranks do not have a good grasp of logical reasoning or of techniques for mathematical proof—they fail to understand syllogisms, they beg the question, they cannot give a proper reductio ad absurdum argument, and so on. Their solutions are often long and convoluted, using nonstandard terminology and notation, and riddled with mathematical errors.
In the eighteenth century, long before any of the problems were proved impossible, false proofs deluged the French Royal Academy of Sciences. They received approximately 150 articles on squaring the circle between 1741 and 1775. The members of the academy believed— even without a rigorous proof—that the problems were impossible. As early as 1701 they wrote, “If the geometers dared to pronounce without absolute demonstrations, and were satisfied with the strongest probabilities, they would have come to the decision a long time ago with one voice that the quadrature of the circle is impossible.”

In 1740 Louis Castel (1688–1757) wrote, “It is not the famous geometers, the true geometers who seek the squaring of the circle: They know too much about it. It is the half-geometers who hardly know Euclid.” In fact, members of the academy were so tired of being inundated with quackery that in 1775 they passed a resolution not to accept solutions to the problems of circle squaring, angle trisection, or cube doubling. (They also resolved not to accept proposals of perpetual-motion machines.)
The mathematical physicist John Baez (1961–) proposed a “crackpot index” that was intended to provide “a simple method for rating potentially revolutionary contributions to physics.” The individual begins with a score of −5. Then Baez presented a list of thirty-seven characteristics of a crackpot. Each time a criterion is met, a prescribed number of points is added to the index.
Mathematician Chris Caldwell was inspired by Baez’s list and devised a mathematical version. Some (lightly edited) examples from Caldwell’s list are
- 1 point for each word in all capital letters;
- 5 points for every statement that is clearly vacuous, logically inconsistent, or widely known to be false;
- 10 points for each such statement that is adhered to despite careful correction;
- 10 points for not knowing (or not using) standard mathematical notation;
- 10 points for expressing fear that your ideas will be stolen;
- 10 points for each new term you invent or use without properly defining it;
- 10 points for stating that your ideas are of great financial, theoretical, or spiritual value;
- 10 points for beginning the description of your work by saying how long you have been working on it;
- 10 points for each favorable comparison of yourself to established experts;
- 10 points for citing an impressive-sounding, but irrelevant, result;
- 20 points for naming something after yourself;
- 30 points for not knowing how or where to submit their major discovery for publication;
- 30 points for confusing examples or heuristics with mathematical proof;
- 40 points for claiming to have a “proof” of an important result but not knowing what established mathematicians have done on the problem.
Underwood Dudley (1937–) is the modern heir to De Morgan. He spent years collecting stories of mathematical cranks and wrote several humorous books and articles showcasing cranks he has encountered.
As a joke, Dudley took values of π put forth by circle squarers from 1832 to 1879 (many from De Morgan’s book) and fit a regression line to it. He concluded that π changed according to the function 0.0000056060t + 3.14281, where t is years ad. He concluded that π was, well, π at 10:54 pm on November 10, 219 bc.

After his many years studying mathematical cranks, Dudley realized that they fit a pattern. In his book The Trisectors, he presented the following characteristics of the typical angle trisector (and presumably the circle squarers fit a similar mold):
- They are male.
- They are old, often retired.
- They don’t understand what it means for something to be mathematically impossible.
- Their mathematical background is minimal; it most likely ended with high-school geometry.
- They believe that the trisection of an angle is an important problem needing to be solved and that they will be richly rewarded with money or prestige for their work.
- Their proofs are always accompanied by dense, complicated figures.
- It is often impossible to convince them of their errors.
- They are prolific and persistent correspondents who will take up as much time as you give them.
Dudley concluded his description of these cranks by writing, “Now, will you know a trisector when you see one coming? And will you know what to do? Here is a hint: what you do involves your legs. No, you do not kick him.”
Alas, Dudley did not take his own advice. In the 1990s he was sued by one of the individuals that he featured in his book Mathematical Cranks—one William Dilworth. The Federal District Court in Wisconsin threw the case out, but Dilworth appealed. The Seventh Circuit Court of Appeals found for Dudley. Dilworth then sued Dudley in a Wisconsin state court. Dilworth ended up losing and having to pay $7,000 for the defense’s legal expenses.
Excerpted from Tales of Impossibility: The 2000-Year Quest to Solve the Mathematical Problems of Antiquity by David S. Richeson. Copyright © 2019 Princeton University Press. Reprinted by permission.
